Опыт — это не то, что происходит с вами;
это то, что вы делаете с тем, что происходит с вами.
Исаак Ньютон
Ранее я давал базовую модель по добыче нефти сланцевых месторождений США и еще раньше аналогичную модель по добычи нефти в мире.
По просьбам трудящихся даю описание математической модели для таких расчетов, хотя в принципе они хорошо известны и применяются при проектировании и моделировании разработки нефтяных месторождений.
Для расчета модели необходимо знать динамику двух показателей:
— текущей добычи нефти от времени (годам, месяцам или другим периодам) выбранного для анализа объекта Qн(t), t=1..n
— добычи нефти новых скважин от времени того же объекта qн(t)
Расчет добычи нефти по модели Q(t) строится следующим образом:
— для каждого t вычисляется вклад добычи нефти новых скважин в месяце t и всех последующих по формуле
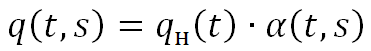 , s=t..n
, s=t..n
![]() — функция, определяющая темп падения новой добычи нефти в заданном месяце
— функция, определяющая темп падения новой добычи нефти в заданном месяце
— для получения текущей добычи по модели Q(t) для каждого t суммируются все предыдущие, вычисленные по модели, вклады q(s, t), s=1..t
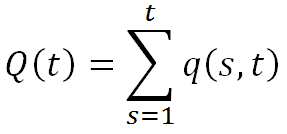 , s=t..n
, s=t..n
— для определения функции ![]() используется минимизация функционала невязки:
используется минимизация функционала невязки:
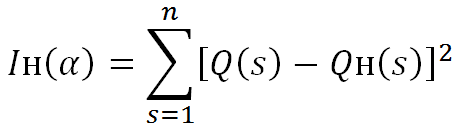
где неизвестной является функция ![]()
— для быстрого поиска этой функции берется сначала функция, равная константе, затем немного усложняется при анализе корреляции базовой модели и фактических данных
Так для первого случае при выборе константы было хорошо видно, что идет систематическое отклонение данных, которое исправлялась заменой функции ![]() на монотонную прямую и позже добавился еще один параметр, которой более точно учитывал входную добычу на начала 2007 года, в итоге эта функция имела всего 3 настраиваемых параметра.
на монотонную прямую и позже добавился еще один параметр, которой более точно учитывал входную добычу на начала 2007 года, в итоге эта функция имела всего 3 настраиваемых параметра.
Однако во втором примере я построил модель даже не зная добычи новых скважин по годам. Для этого я задал экспертно саму функцию ![]() , предполагая ускорение извлечения нефти из пласта. В этом случае добыча новых скважин вычисляется обратным счетом.
, предполагая ускорение извлечения нефти из пласта. В этом случае добыча новых скважин вычисляется обратным счетом.


Уведомление: Модель добычи газа по сланцевым месторождениям США | Через тернии к звездам